VALID Padding (No Padding)
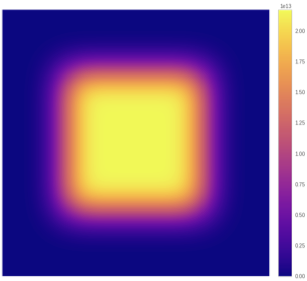This method restricts convolution within the proper dimensions of the image.
With a kernel size larger than 1x1, the output the method computes is smaller than the input and the foveation effect is strong.
Processing the input over multiple layers rapidly increases the foveation effect.
Larger kernel sizes or dilation factors further amplify the foveation effect.
Input (left top corner of an image):
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Zero Padding (SAME)
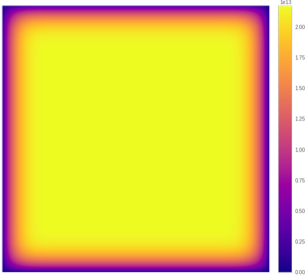This is the most common solution to compute an output of the same dimensions as the input.
With a 3 × 3 kernel, the needed padding amount is 1-pixel, and these pixels are filled with zeros.
The foveation effect is mild, compared with VALID padding.
Larger kernel sizes or dilation factors further amplify the foveation effect.
Input (left top corner of an image):
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Zero Padding (FULL)
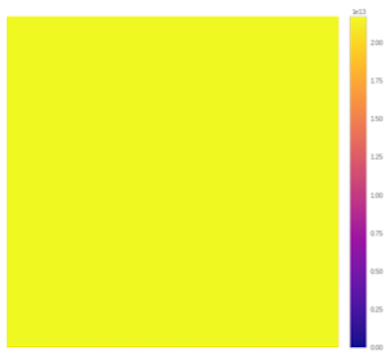This padding mode warrants that the filter is applied whenever it overlaps with the input, even partly.
With a 3 × 3 kernel, the needed padding amount is 2 pixels, and these pixels are filled with zeros.
As a result, every pixel is involved in the same number of convolution operations, leading to a uniform foveation map.
However, the output of the convolution is larger than its input, which can be problematic (e.g. preventing the use of residual connections or inception modules).
Input (left top corner of an image):
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Circular Padding
This SAME-padding method effectively applies circular convolution: Once the kernel hits one side, it can seamlessly operate on the pixels of the other side.
Circular convolution hence renders the feature map as infinite to the kernel, warranting that edge pixels are treated in the same manner as interior pixels.
It is straightforward to prove that the algorithm warrants equal treatment of the pixels irrespective of the kernel size or dilation factor.
Input Image:
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Mirror Padding (SYMMETRIC)
Like circular padding, this SAME-padding method also warrants that each pixel is involved in the same number of convolutional operations.
However, unlike under circular convolution, these operations do not utilize the kernel pixels uniformly (e.g. compare pixels "a", "b", "f", and "g").
The numbers warranty holds with a larger kernel size or under dilation, check that for yourself!
Input (left top corner of an image):
#conv_ops each pixel is involved in:
The map looks uniform, but the cells in the kernel are not utilized uniformly (e.g. pixel a).
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Not all cells are utilized.
Mirror Padding (REFLECT)
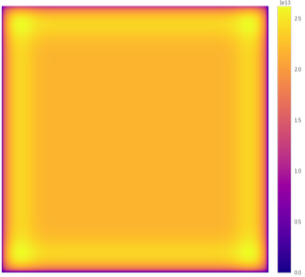This SAME-padding method mirrors the edges starting from the 2nd pixel, i.e., without including the border pixels.
This reduces the contribution of these pixels and over-emphasizes the contribution of the inner pixels adjacent to them.
Input (left top corner of an image):
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Replication Padding
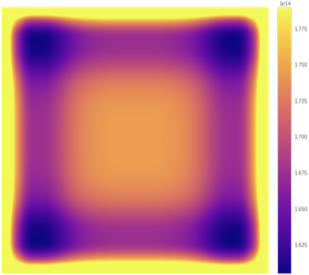This SAME padding replicates the border pixels only to fill the needed padding area.
With a 1-pixel padding area, the result is equivalent to SYMMETRIC mirror padding.
However, for a 2-pixel padding area (needed with a 5 × 5 kernel), the method overemphasizes the border pixels at the cost of reducing contributions of the inner pixels adjacent to them.
Input (left top corner of an image):
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =
Partial Convolution
This method avoids explicit padding by treating the padding area as missing pixels.
The convolution computed at each location only sums contributions of valid pixels, and reweighs the computed sum in case padding pixels were present.
Due to the weights used, the foveation behavior is analogous to REFLECT mirror padding.
Input (left top corner of an image):
#conv_ops each pixel is involved in:
Step-by-step illustration
Display conv operations that involve the selected pixel:
Padded Input:
Kernel cells involved:
sum =